泊松分布预测足球进球数（泊松分布进球概率对照表）

泊松回归的简介

泊松回归，并假设它期望值的对数可被未知参数的线性组合建模。泊松回归模型有时（特别是当用作列联表模型时）又被称作对数-线性模型。2014年世界杯，所有的数据分析专家都以数据为准，分析员最后都会将其整合成模型。

足球比赛结果用泊松分布准确率高吗

泊松分布适合于描述单位时间（或空间）内随机事件发生的次数 你算出了进球率也猜不了一场球能进多少的，进球多少受太多因素影响了。

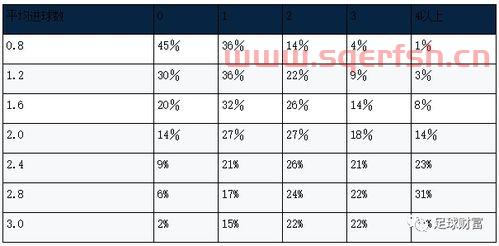
根据泊松分布，足球比赛的结果同样具有分散性。一支足球队进1或2个球的可能性更大，其次为不进或者进3个，而进4或5个球(或者更多)的几率则大大下降。

主队单场3球——泊松分布计算结果是160%，实际情况是134%。主队单场3球——泊松分布计算结果是160%，实际情况是134%。

能举例列出足球泊松分布的例子吗?谢谢

1、泊松分布是最重要的离散分布之一，它多出现在当X表示在一定的时间或空间内出现的事件个数这种场合。在一定时间内某交通路口所发生的事故个数，是一个典型的例子。泊松分布的产生机制可以通过如下例子来解释。

2、泊松分布适合于描述单位时间（或空间）内随机事件发生的次数 你算出了进球率也猜不了一场球能进多少的，进球多少受太多因素影响了。

3、离散概率分布的例子有伯努利分布（Bernoulli distribution）、二项分布（binomial distribution）、泊松分布（Poisson distribution）和几何分布（geometric distribution）等。

4、让我们考虑这个平均每天发生2起事故的例子。泊松分布的实现和二项分布有些类似，在泊松分布中我们需要指定比率参数。泊松分布的输出是一个数列，包含了发生0次、1次、2次，直到10次事故的概率。我用结果生成了以下图片。

5、原因主要在于泊松近似公式，以及更重要的，原于该近似公式的泊松分布，分布的重要性和知名度在离散型分布中仅次于二项分布。

直接对比法得出的比表面与BET比表面有何差别？

1、两种 *** 都是使用低温氮吸附 *** 侧固体比表面积；直接对比法是用所测样品和氮气标准样品的氮气脱附量的比值得到样品的比表面积值；单点BET是多点BET方程的简略，是通过BET方程计算得出来的，不需要标准样品。

2、其中BET理论在比表面计算方面在大多数情况下与实际值吻合较好，被比较广泛的应用于比表面测试，通过BET理论计算得到的比表面又叫BET比表面。

3、BET比表面积测试可用于测颗粒的比表面积、孔容、孔径分布以及氮气吸附脱附曲线。对于研究颗粒的性质有重要作用。当液氮被取走时，样品管重新处于室温，吸附氮气就脱附出来，在屏幕上出现脱附峰。

4、“直接对比法”测定比表面积有一个局限性，即被测样品与标准样品的吸附特性必须一致，否则测定的精确性会受到影响。BET比表面的测定 *** 则没有上述的局限性。

5、BET是该理论的三个提出者姓氏的首字母缩写。由于BET法适合大部分样品，目前成为更流行的比表面分析 *** 。

6、比表面积越大，称样量越小，反之，比表面积越小，称样量越大。BET方程为线性方程，只有称样量合适，实验所得的数据的线性越高，所得的BET比表面积就越准确。固体有一定的几何外形，借通常的仪器和计算可求得其表面积。

怎么算买足球概率更大标准差计算

首先，根据开奖号码统计每个号码出现的次数；其次，计算每个号码出现的概率，令P(n)表示号码n出现的概率；然后，根据概率，计算离散指数：DI=∑n=1nP(n)2；最后，计算出现概率的标准差：SD=√DI(1DI)。

计算标准差的步骤通常有四步：计算平均值、计算方差、计算平均方差、计算标准差。

足球胜平负全买计算公式如下：返奖率：1÷（1÷胜+1÷平+1÷负）=返奖率。原始赔率：100÷（返奖率÷胜、平、负的欧赔）=原始赔率。胜率的计算公式：1÷欧赔=打出几率。

免责声明
           本站所有信息均来自互联网搜集
1.与产品相关信息的真实性准确性均由发布单位及个人负责，
2.拒绝任何人以任何形式在本站发表与中华人民共和国法律相抵触的言论
3.请大家仔细辨认！并不代表本站观点,本站对此不承担任何相关法律责任！
4.如果发现本网站有任何文章侵犯你的权益,请立刻联系本站站长[ *** :775191930]，通知给予删除